Circles

Circles appear everywhere in maths. Mathematicians just can’t get enough of them.

Here, we’re going to introduce a few of the terms used to describe parts of a circle, and then we’re going to look at calculating the area and perimeter/circumference of a circle. The terms we’ll need are shown on the diagram and described in further detail below.

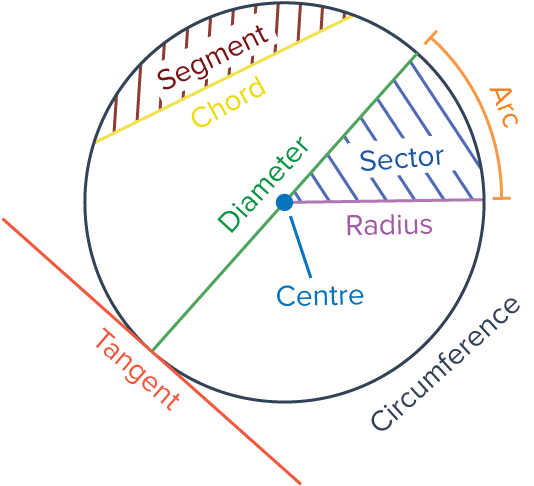
Key Circle Terms

• The circumference is the outside edge of the circle.
• A diameter is a straight line going straight through the centre of the circle and touching the circumference at each end.
• A chord is a straight line joining any two parts of the circumference.
• A segment is the area bound by the circumference and a chord.
• An arc is a section of the circumference.
• A radius (plural radii, pronounced “ray-dee-eye”) is a straight line joining the centre to the circumference.
• A sector is the area bound by two radii and an arc – like a pizza slice.
• A tangent is a straight line that touches the circumference at a single point.

Area and Circumference of a Circle

Area of a circle =\textcolor <\pi>\textcolor^2

Circumference of a circle =\textcolor <\pi>\textcolor = 2\textcolor<\pi>\textcolor

Where \textcolor is the radius, \textcolor is the diameter, and \textcolor <\pi>is a very special number with a specific value of 3.14159265. ( 3.14 to 2 dp).